[Programmers, python3, Lv.3] 아방가르드 타일링

문제

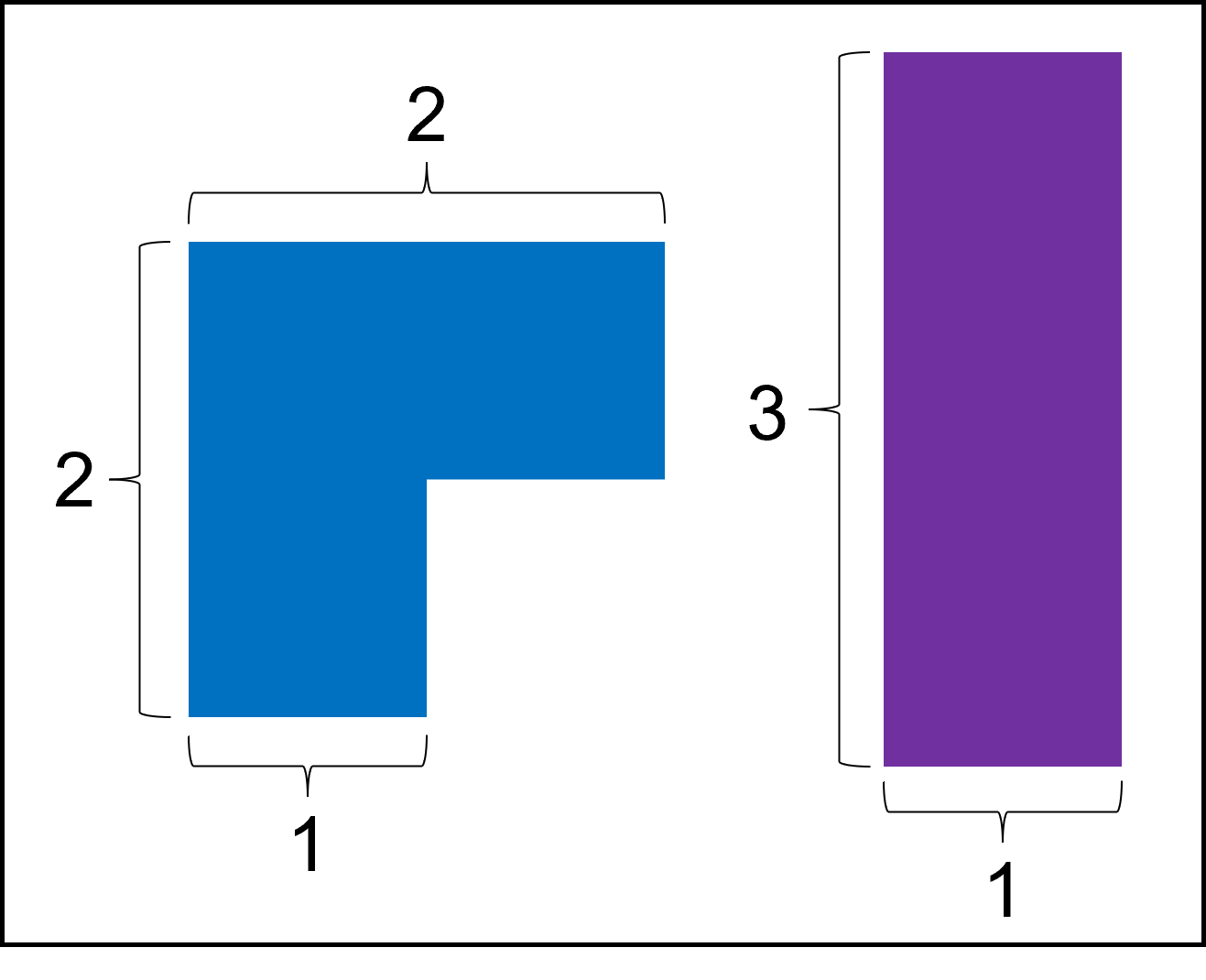
n이 주어졌을 때, 이 두 가지 종류의 타일로 n x 3 크기의 판을 타일링하는 방법의 수를 return 하도록 solution 함수를 완성해주세요.

풀이

새로운 타일링 방법

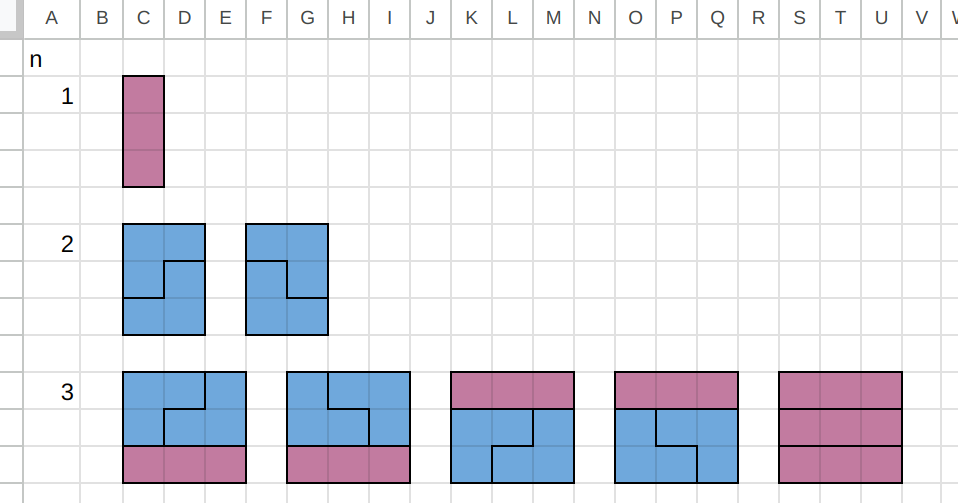
먼저 두 종류의 타일로 n 크기의 판을 타일링 하는 새로운 방법의 수는 다음과 같다.
이 방법들을 제외하면 나머지는 전부 이 방법들을 조합해서 만들 수 있다.

1에서 6까지는 다음과 같다.

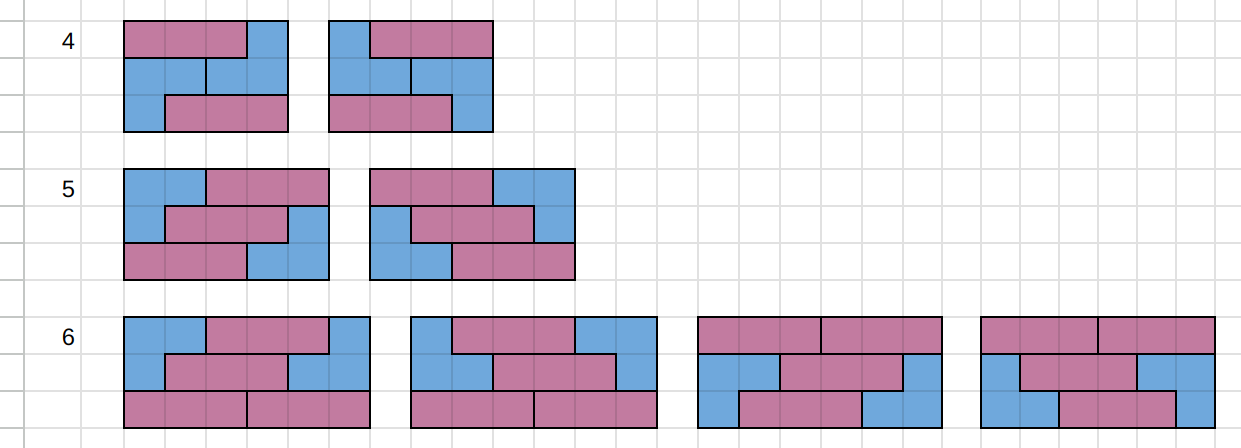
n7부터는 4에서 6까지 방법에 가로로 1x3 타일만 추가된다.

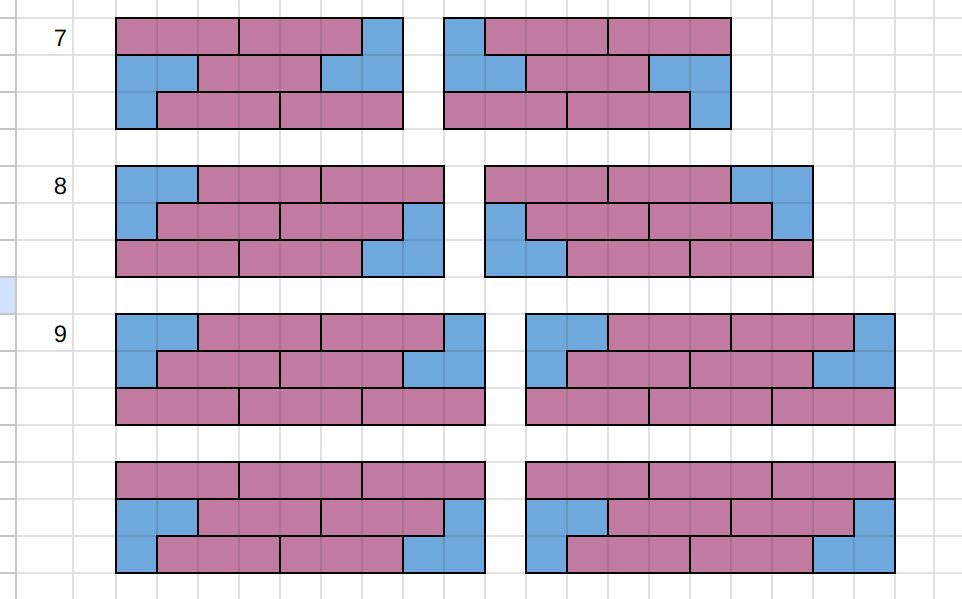
따라서 n7 부터는 새로운 타일링 방법이 2,2,4로 반복된다.

n	1	2	3	4	5	6	7	8	9	10
new	1	2	5	2	2	4	2	2	4	…

점화식

이것을 토대로 점화식을 구해야 한다.

먼저 n이 1,2,3일때 새로운 방법 수를 N1,N2,N3 이런 식으로 쓰고.
n이 3일 때 모든 경우의 수를 망라하면 다음과 같다.

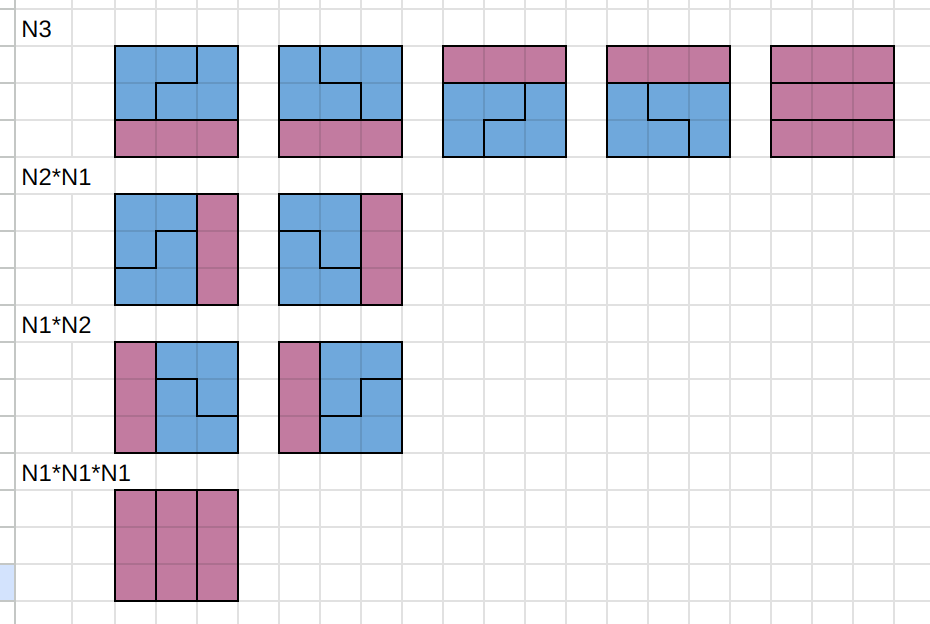
같은 방식으로 n이 4일때 모든 경우의 수를 망라해보면 다음과 같다.

N4
N3*N1
N2*N2
N2*N1*N1
N1*N3
N1*N2*N1
N1*N1*N2
N1*N1*N1*N1

여기서 규칙성을 발견 할 수 있다.
n에 따른모든 경우의 수를 Sn이라고 쓰겠다.

S4
= N4
+ N3 * S1
+ N2 * S2
+ n1 * S3

일반화하면 다음과 같다.

$Sn = N_1 * S(n-1) + N_2 * S(n-2) + N_3 * S(n-3) +…+ N_n * S_1 + Nn$

이 공식을 그대로 적용해도 정답은 맞게 나오지만 계산량이 많아
다이나믹 프로그래밍을 사용해도 n이 커지면 시간초과로 통과하지 못하는 경우가 생긴다.

따라서 좀더 간단한 공식이 필요하다.

n3 이후로는 2,2,4가 반복되기 때문에 이를 이용해 식을 줄일 수 있다.
S(n+3)을 위에서 나온 공식에 대입한다.

$S(n+3) = N_1 * S(n+2) + N_2 * S(n+1) + N_3 * S(n) + N_4 * S(n-1) + N_5 * S(n-2)+…$

여기서 Nn에 숫자를 대입한다.

$S(n+3) = S(n+2) + 2S(n+1) + 5S(n) + 2S(n-1) + 2S(n-2) + 4S(n-3) +…$

그다음 Sn에서 S(n+3)을 뺀다.

$S_n - S(n+3) = - S(n+2) - 2S(n+1) - 5S(n) - S(n-1) + S(n-3)$

최종적으로 S(n+3)을 기준으로 식을 정리하면 아래와 같다.

$S(n+3) = S(n+2) + 2S(n+1) + 6S(n) + S(n-1) - S(n-3)$

코드

위 과정에서 나온 점화식을 자신의 코드로 옮기면 된다.
내가 사용한 방법은 n=6까지는 미리 기록해 두고
주어진 n까지 계산해서 올라가는 방법을 사용했다.

def solution(n):
    dict_solution = {1:1, 2:3, 3:10, 4:23, 5:62, 6:170}     
    if n in dict_solution: return dict_solution[n]

    for i in range(7,n+1) :
        res = 0
        res -= dict_solution[i-6]
        res += dict_solution[i-4]
        res += 6*dict_solution[i-3]
        res += 2*dict_solution[i-2]
        res += dict_solution[i-1]
        dict_solution[i] = res

    return answer%1000000007